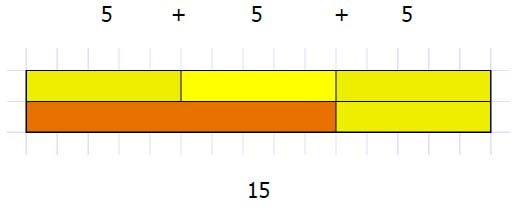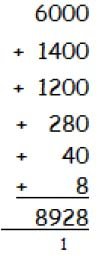Multiplication Stages
Stage 1: Pictures and Objects
Children are encouraged to develop a mental picture of the number system in their heads to use for calculation. They develop ways of recording calculations using pictures and real objects, etc.
 e.g. How many shoes are there altogether?
e.g. How many shoes are there altogether?
Give each child 3 buttons on their top. How many will you need?
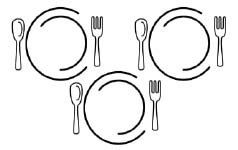 Each plate has 2 carrots on, how many carrots are there altogether?
Each plate has 2 carrots on, how many carrots are there altogether?

Stage 2: Repeated Addition
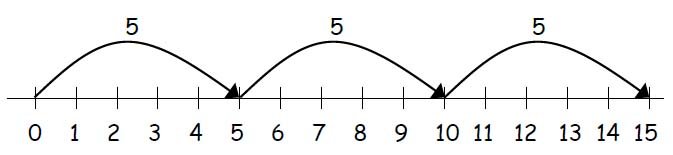
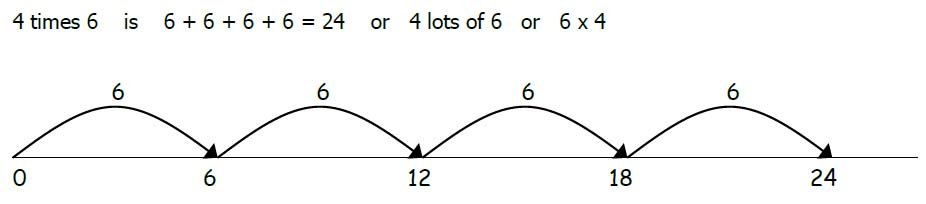
The number line is used as an effective informal method of written multiplication to show multiplication as repeated addition.
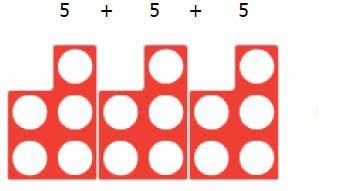
5 times 3 is 5+5+5=15 or 3 lots of 5 or 5x3
5 x 3 means 5, 3 times. Any language needs to match the visual image that is being used.
Initially, Numicon plates and Cuisenaire rods can be used to represent the repeated addition.
|
|
|
Following this, the repeated addition is shown on a number line as jumps.
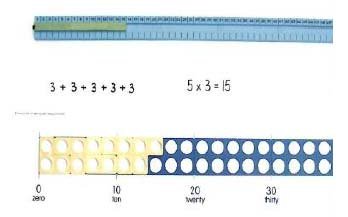 Cuisenaire rods and number tracks can be used to illustrate the repeated addition alongside the Numicon plates. The number track replicates the layout of the number line.
Cuisenaire rods and number tracks can be used to illustrate the repeated addition alongside the Numicon plates. The number track replicates the layout of the number line.
Children should know that 3 x 5 has the same answer as 5 x 3. This commutativity can also be shown on the number line.
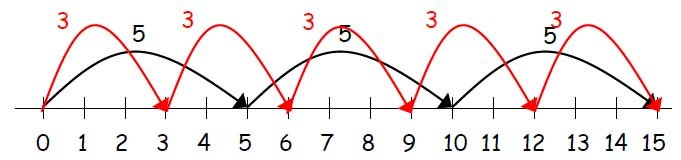
Stage 3: Arrays
C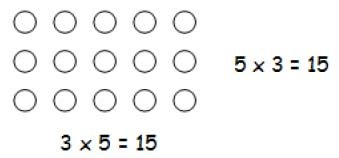 hildren should be able to model a multiplication calculation using an array. This knowledge will support with the development of the grid method later on.
hildren should be able to model a multiplication calculation using an array. This knowledge will support with the development of the grid method later on.
This method will be supported by the use of practical resources to create strong visual images e.g. Cuisenaire rods, counters, objects in the environment.
 The commutative principle of multiplication will be taught alongside arrays as shown here clearly through the use of Cuisenaire.
The commutative principle of multiplication will be taught alongside arrays as shown here clearly through the use of Cuisenaire.
 Counters are used to represent arrays.
Counters are used to represent arrays.
Stage 4: The Empty Number Line for Repeated Addition
Most children should be able to use an empty number line by the end of Year 2.
Children will continue to use repeated addition but will progress onto using a blank number line:
Stage 5: The Grid Method
Children’s earlier use of arrays as a representation for multiplication leads on to the grid method as the first formal written method of multiplication.
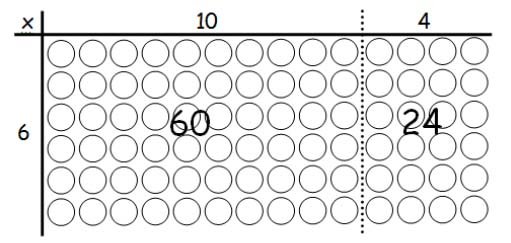
This is then supported further using Dienes apparatus and Cuisenaire rods to reinforce the place value of the numbers involved. Through the use of the practical resources, children will be able to access the written grid method from Year 2 and 3 upwards. Most children should be secure in the use of written grid method for multiplication by the end of Year 4 for the multiplication of TU and HTU x U.
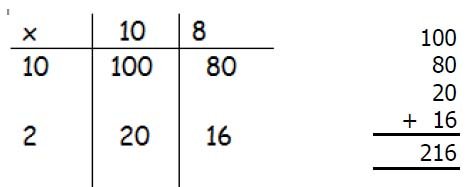
TU x U
e.g. 16 x 4
 The use of practical resources runs alongside the written recording in the grid format.
The use of practical resources runs alongside the written recording in the grid format.
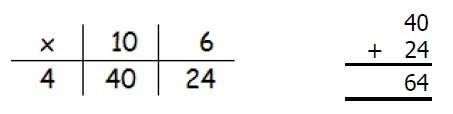
TU x TU
e.g. 12 x 18
|
|
|
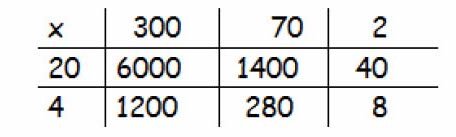
HTU x TU
e.g. 372 x 24
|
|
|
By this stage, children will be using the grid method solely as a written method for multiplication, without the need for practical resources to create visual images.
This method can also be applied easily to the multiplication of decimal numbers.
TU x U.t
e.g. 42 x 3.7
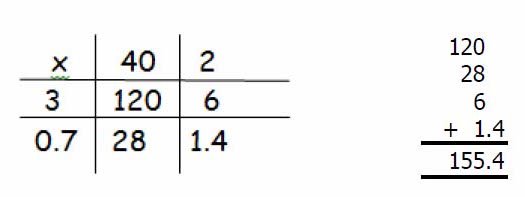
Please click on the link below to watch a video modelling the 2 digit by 2 digit grid method multiplication strategy.
Multiplication 2 digit by 2 digit grid method
Stage 6: Expanded Short Multiplication
It is important that children maintain a secure method for multiplication into Year 5 – most children will move on to using short multiplication with the expanded format as an interim stage.
The next step is to represent the method of recording in a column format, but showing the working. This method should be presented to the children alongside the grid method, and similarities between the two methods should be highlighted.
Children should describe what they do by referring to the actual values of the digits in the columns. For example, the first step in 38 × 7 is ‘thirty multiplied by seven’, not ‘three times seven’, although the relationship 3 × 7 should be stressed.
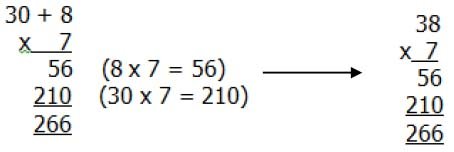
Stage 7: Short and Long Multiplication
The recording is reduced further, with carry digits recorded below the line for calculations using TU x U.
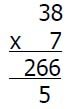
Children who are already secure with multiplication for TU × U and TU × TU should have little difficulty in using the same method for HTU × TU. This formal algorithm will be taught from year 5. Most children will be secure in using this method to multiply up to 4 digit numbers by 2 digit whole numbers by the end of year 6.
Again, the importance of recognising the place value of the digits involved will be stressed. e.g. 20 x 6, 20 x 80 and 20 x 200; the relationship between 2 x will inevitably be utilised.
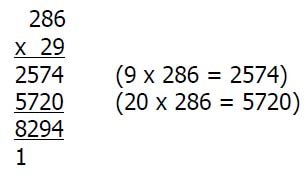
As an intermediate step, each stage of the multiplication can be explicitly recorded in an expanded form to show the separate products. These intermediate products are then totalled at the end, as in the standard compact algorithm.
Please click on the link below to watch the videos;
modelling the 3 digit by 2 digit (expanded brackets) multiplication strategy.
multiplication 3 digit by 2 expanded brackets
modelling the 3 digit by 2 digit long multiplication strategy.
multiplication 3 digit by 2 digit long multiplication
- Rectory Gardens, Worthing
West Sussex, BN14 7TQ - OFFICE@BROADWATERCE.ORG
- 01903 235389